20.5 Bleichenbacher attack

Long before Bleichenbacher published this work, it was well known that plain RSA is vulnerable to chosen-ciphertext attacks. If Eve wants to decrypt the ciphertext c ≡ md (mod n) that Bob encrypted for Alice, she can choose a random integer s and ask Alice to decrypt an apparently innocuous message c′≡ sec (mod n).

If Alice, thinking she is decrypting ciphertexts received from a legitimate party such as Bob, returns Eve the result m′≡ (c′)d (mod n), Eve can easily recover the original message m by computing m ≡ m′s−1 (mod n). This works because:

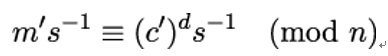
and for the term (c′)ds−1 it holds that:

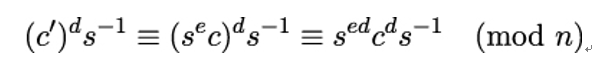
Moreover, because ed (mod n) ≡ 1 by the definition of the RSA algorithm, Eve can easily determine m because:

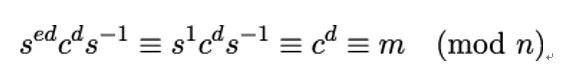
In his publication [34], Bleichenbacher showed that Eve can also decrypt any ciphertext c if she has access to an oracle that for every ciphertext returns whether the corresponding plaintext has a valid PKCS #1 padding.

20.5.1 The attack

Bleichenbacher’s attack is based on the observation that any plaintext m that has a valid PKCS #1 padding is larger than or equal to the k-byte number 00 02 … 00 and less than the k-byte number 00 03 … 00.

In other words, if we define number B = 28(k−2) – which is an 8(k − 2)-bit number with the binary representation 100 … 00 – then for every m with a valid PKCS #1 padding, it holds that:

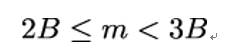
As a result, if Eve can trick Alice into decrypting some ciphertext c′ = cse = m′e (mod n) and learns that the corresponding plaintext m′ = ms has a valid PKCS #1 padding, then Eve knows that:

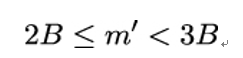
and since m′ = ms (mod n), the preceding inequality can be rewritten as:

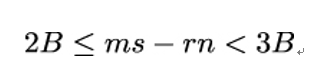
Next, note that the definition of the modulus operator states that there exists an integer r such that:

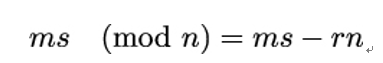
and we can therefore rewrite the inequality once again as:

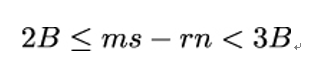
By subtracting the term ms, we can further simplify the inequality to obtain a representation where only the middle term contains an unknown:

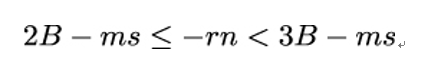
As you can easily verify, we can further simplify the inequality by first multiplying it by −1 and then dividing it by n:

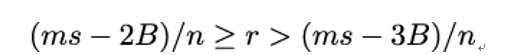
That still leaves us with an inequality with two unknown terms r and m. However, we known that m is limited to the interval 2B ≤ m < 3B. Therefore, we can replace ms in the left term with 3B and replace ms in the right term with 2B to obtain:

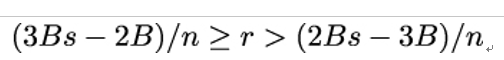
Eve starts the attack by generating a large number of random integers s0,s1,s2,… and letting Alice, the padding oracle, decrypt ciphertexts cs0,cs1,cs2,…. For every csi whose corresponding plaintext has a valid PKCS #1 padding, Eve computes the interval for ri using inequality 20.5.1 and adds ri to the set R.

In the next step, Eve computes intervals for the plaintext m she wants to obtain by plugging in the values ri ∈ R into inequality 20.5.1

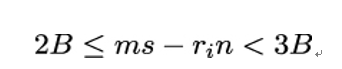
which she transforms into:

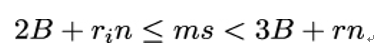
and, finally, into:

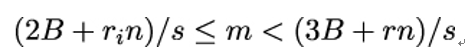
Eve keeps only those intervals for m that intersect with the interval 2B ≤ m < 3B. By obtaining more and more such intersections, Eve eventually determines an interval spanning only a single value, namely the plaintext m she wants to obtain.

Figure 20.4 illustrates Eve’s strategy to determine the unknown plaintext m. Initially, m is confined to the interval 2B ≥ m < 3B. In the second step, Eve determines the intervals for r0 and keeps only their intersection with the original interval 2B ≥ m < 3B. The intersection is smaller than the original interval.

In every subsequent step, using the corresponding ri value, Eve determines new intervals for m and their intersection with the interval from the previous step. This way, the interval where m is located gets smaller with every step and eventually contains a single value, namely the unknown plaintext m.

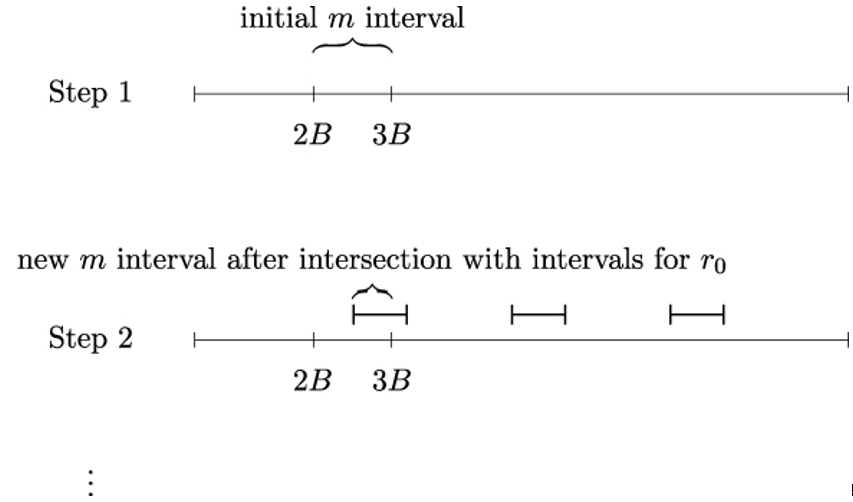
Figure 20.4: Determining plaintext m as the intersection of intervals

In the two decades after its publication, Bleichenbacher’s attack turned into the foundation of all oracle attacks on RSA-based TLS handshakes.